High-Order Finite Element Methods - Dr Sascha Duczek

Dr Duczek’s primary research interests are:

• High-Order Finite Element Methods,
• Fictitious Domain Methods, and
• Structural Dynamics.

His work involves both fundamental research regarding the basic principles of the underlying methods, and their exciting applications. The overarching goal of his research activities - outlined below - is to develop highly efficient numerical methods to predict the dynamic response of complex structures.

These proposed methods can be used to simulate and therefore predict the behaviour of our aging civil infrastructure and hence, to help increase the safety of the public.

In particular, one topic of utmost importance is the continuous monitoring of old bridges to predict occurring damages at an early stage.

High-Order Finite Element Methods

High-Order Finite Elements have been deeply researched since their inception in the 1970s - see Szabó, Babuška, and Peano [1, 2, 3, 4]. The main advantage of these methods is their fast convergence to accurate solutions. Compared to Low-Order Finite Element Methods which are used in virtually all commercial finite element software packages, a much faster convergence at significantly reduced costs can be attained (see Figure 1).using High-Order Elements.

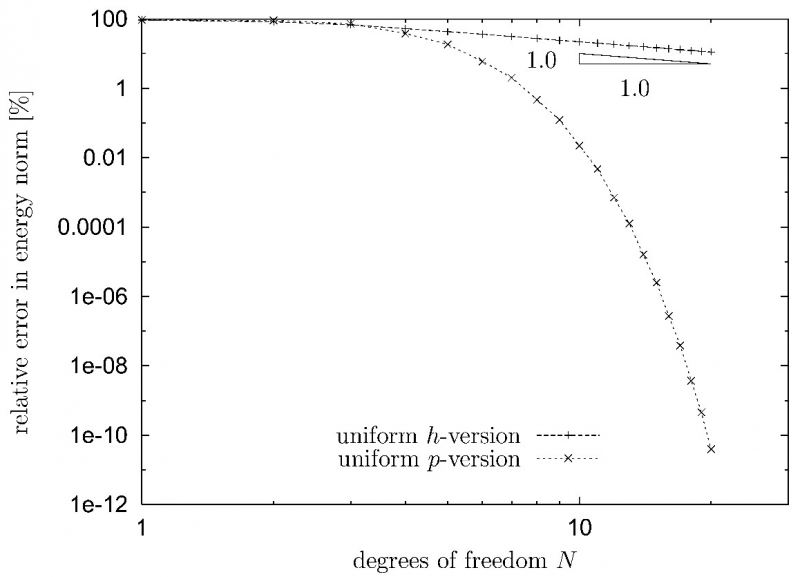
Figure 1: Comparison of the h- and p-version: Relative error in the energy norm

In this context, Dr Duczek is interested in the performance of different types of shape functions which determine important aspects of each of the high-order methods.

Nowadays, the p-version of the FEM (hierarchic Legendre polynomials) [4], the Spectral Element Method (SEM; Lagrange polynomials) [5, 6], and the Isogeometric Analysis (IGA; B-splines, NURBS) [7] are widely adopted. Each of these methods has individual advantages that make them attractive for certain areas of application.

The p-FEM possess an inherent p-adaptivity feature due to the hierarchic nature of the shape functions, i.e. the polynomial degree of the finite elements can be easily changed from element to element without sacrificing the compatibility between adjacent elements [8].

The distinctive property of the SEM that sets it apart from the other high-order methods is the possibility to straightforwardly diagonalize the mass matrix by numerical integration and still retain the optimal rates of convergence [9]. This property makes the SEM very attractive for dynamical applications including wave propagation analysis, earthquake engineering, impact and crash test simulations, etc.

The exceptional feature of IGA is that it is possible to construct finite elements with higher continuity, i.e. for adjacent elements, not only the displacements themselves are continuous, but also their derivatives. IGA also offers an easy integration of Computer Aided Design software into the simulation pipeline.

Each high-order method must be carefully selected, for its suitability with the intended area of application.

Fictitious Domain Methods

The fundamental idea of fictitious domain methods (also known as embedded domain methods) is to relieve analysts from the necessity of generating finite element meshes that are geometry conforming [10, 11, 12]. Thus, one of the major bottlenecks of the simulation pipeline can be circumvented. The basic approach is illustrated in Figure 2.

These methods are well suited for materials with complex microstructure and image-based analysis and therefore, applications are useful for hip replacements [13] and metallic foams, to give just two examples [14].

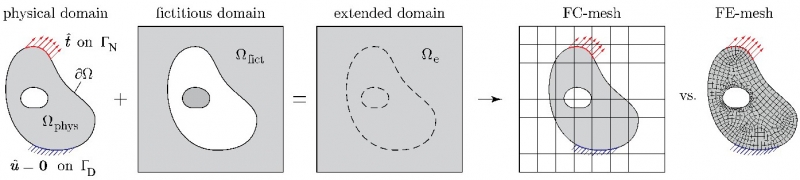
Figure 2: Basic idea of fictitious domain methods

Structural Dynamics

Structural dynamics attempts to solve the equations of motion as efficiently as possible using numerical methods. To this end, implicit and explicit time-integration (time-stepping) are typically employed. While, implicit methods are often unconditionally stable, i.e. an arbitrary time step size (time increment) can be used, they involve the solution of a system of equations in each time step.

In contrast, explicit methods are generally conditionally stable, i.e. a critical time increment is provided, but only involve simple matrix-vector multiplications to advance in time. To fully exploit the advantages of explicit methods the mass matrix associated with the spatial discretization has to be formulated in diagonal form [10, 11].

This is, however, not always possible and therefore, alternative methods need to be devised to diagonalize (lump) the mass matrix [9, 12]. Only then can applications such as wave propagation analysis in the context of earthquake engineering, and structural health monitoring be possible.

Areas of Application:

The methods briefly introduced above have been mainly applied in the context of structural health monitoring (SHM) [18]. The primary objectives of every SHM system are the continuous monitoring of safety-relevant component parts during service and the identification of anomalies or damages such as cracks, delaminations and debondings in structures.

To this end, a network of transducers is integrated into the structure whose function is similar to the human nervous system (see Figure 3).

Figure 3: Analogy of SHM sensor network and human nervous system

An important SHM approach is the use of (guided) wave-based methods, often used due to their sensitivity to small defects. To be able to predict the health status of complex structures, efficient simulation tools, suitable signal processing techniques, and experimental measurements all have to be utilized.

Important research topics that still need to be addressed are depicted in Figure 4.

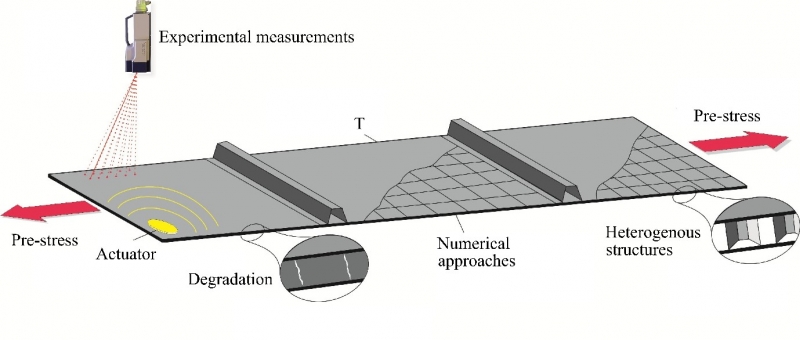
Figure 4: Current research topics in SHM

In this context, robust and efficient numerical methods for wave propagation analysis have been developed based on a combination of SEM and the fictitious domain concept [18, 19, 20]. Exemplary results are depicted in the following.

1)      Three-dimensional wave propagation analysis:

Excitation of guided waves in a three-dimensional plate by means of a circular piezoelectric actuator.  Damage in the form of a conical hole with circular shape is introduced to the plate. The guided waves interact with the defect in the structure and the effect of mode conversion is clearly evident in the displacement field [18] (see Figure 5).

 
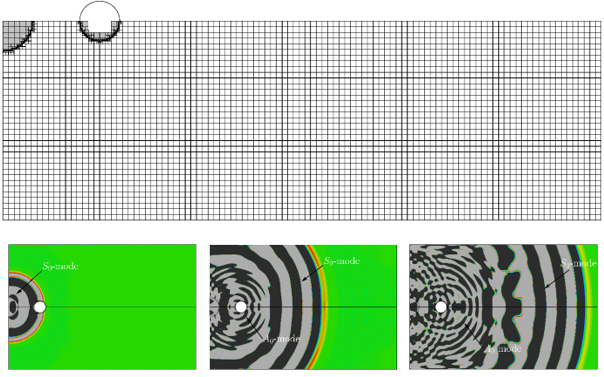
Figure 5: Wave field for a plate with a conical hole

2)      Combination of the Scaled Boundary Finite Element Method (SBFEM developed by Prof Chongmin Song) with fictitious domain methods for efficient elasto-dynamics:

The SBFEM is a very powerful semi-analytical method for the solution of engineering problems [21]. It is very well suited for image-based analysis using quadtree- and octree-meshes [22]. Meshes based on spacetree decompositions have, however, one disadvantage which is related to the geometry representation by a “staircase” curve.

Therefore, a combination with fictitious domain methods yields advantages in terms of geometry approximation and automatization [23]. The basic idea of this hybrid scheme is depicted in Figure 6.

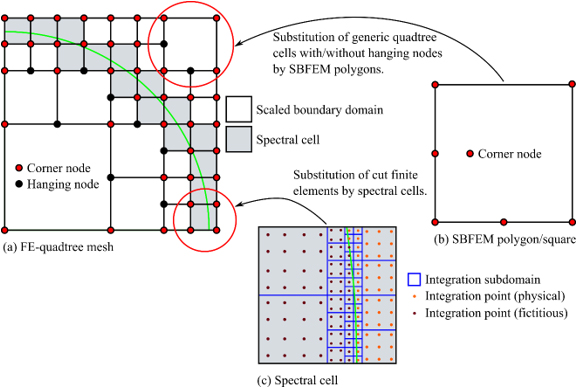
Figure 6: Coupling of SBFEM and SCM (spectral cell method ->fictitious domain method)

This approach can be easily applied to complex examples based on image data or an implicit geometry description. As an example, a modal analysis of a violin plate is shown in Figure 7.