Scaled boundary finite element method

About the Group Numbers of researchers in CIES are doing great work related to SBFEM, the group is led by Professor Chongmin Song - Director of CIES. Chongmin Song, PhD, is a Professor of Civil Engineering and the Acting Director of the Centre for Infrastructure Engineering and Safety at the University of New South Wales, Australia. He is a Member of the General Council of the Asia-Pacific Association of Computational Mechanics (APCOM) and an Executive Member of the Australian Association for Computational Mechanics (AACM). Professor Song is also the co-author of Finite-Element Modelling of Unbounded Media. 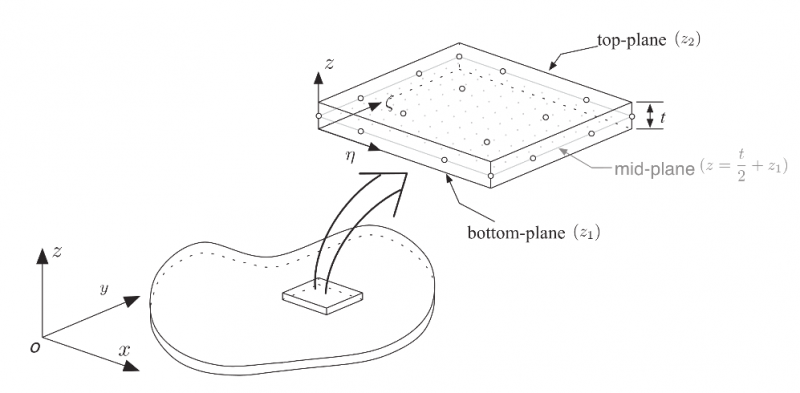Read Professor Song's Profile	About SBFEM The SBFEM is a semi-analytical fundamental-solution-less boundary-element method based solely on finite elements [Wolf & Song 2000]. It not only combines many advantages of the finite-element method and the boundary-element method but also exhibits additional advantages. Much like the finite element method (FEM), the problem domain can be divided into multiple scaled boundary finite elements. Only the boundary of each scaled boundary finite element needs to be discretised, hence reducing the dimension of the problem by one.
About the Book The Scaled Boundary Finite Element Method: Introduction to Theory and Implementation covers the static and dynamic stress analysis of solids in two and three dimensions. The relevant concepts, theory and modelling issues of the scaled boundary finite element method are discussed and the unique features of the method are highlighted. The applications in computational fracture mechanics are detailed with numerical examples. A unified mesh generation procedure based on quadtree/octree algorithm is described. It also presents examples of fully automatic stress analysis of geometric models in NURBS, STL and digital images. Written in lucid and easy to understand language by the co-inventor of the scaled boundary element method Provides MATLAB as an integral part of the book with the code cross-referenced in the text and the use of the code illustrated by examples Presents new developments in the scaled boundary finite element method with illustrative examples so that readers can appreciate the significant features and potentials of this novel method—especially in emerging technologies such as 3D printing, virtual reality, and digital image-based analysis The Scaled Boundary Finite Element Method: Introduction to Theory and Implementation is an ideal book for researchers, software developers, numerical analysts, and postgraduate students in many fields of engineering and science.	Each scaled boundary finite element: Can be polygonal (2D) or polyhedral (3D) shapes Can have arbitrary number of edges (2D) and arbitrary number of edges and surfaces (3D) Must have a point from which the whole boundary is visible (star-convexity criterion) called scaling centre Se more details of research applications below.
Image-based analysis Automatic meshing technique to convert images from computed tomography (CT) scans and ultrasound is developed based on octree hierarchical structure. The resulted octree mesh is highly compatible with SBFEM for various numerical analyses.
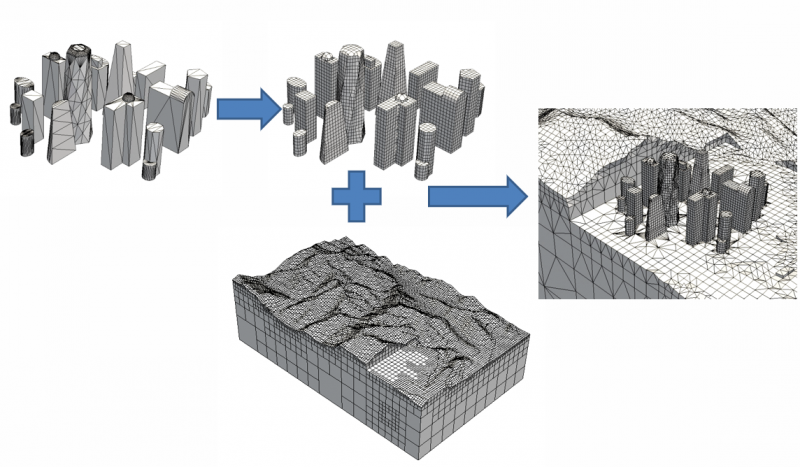
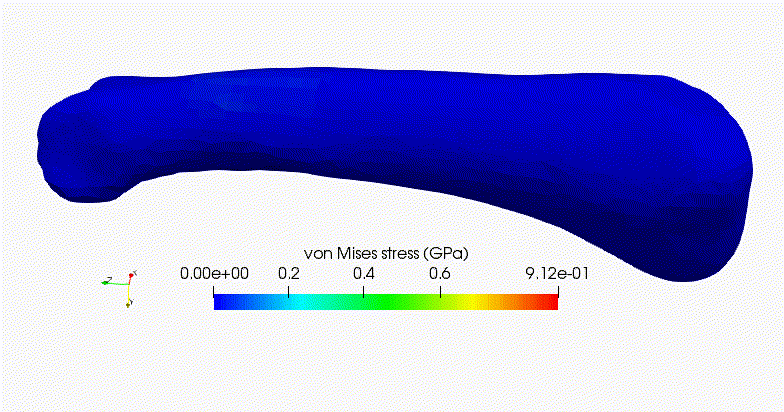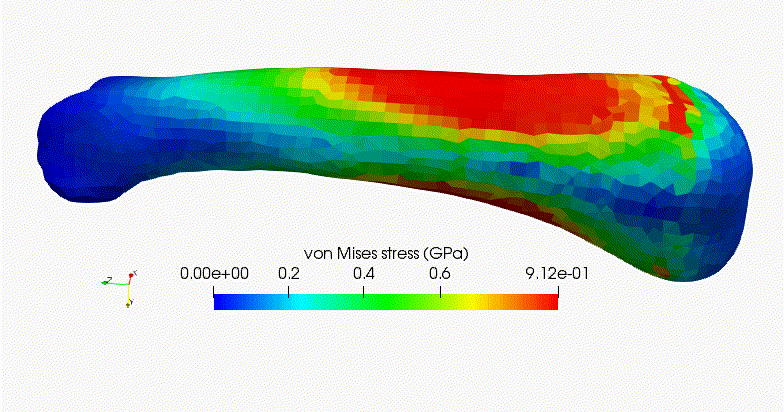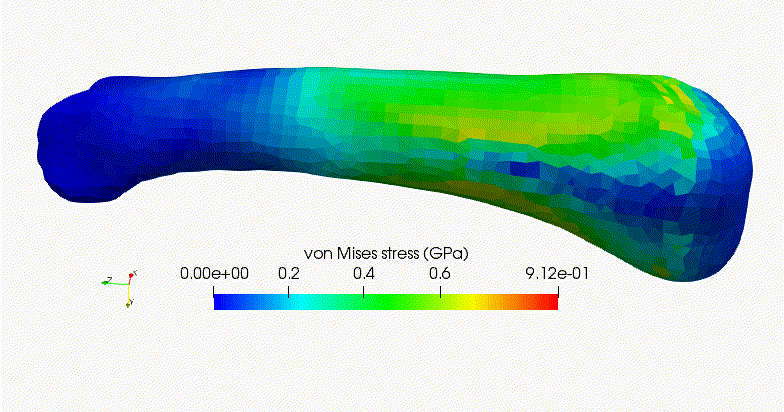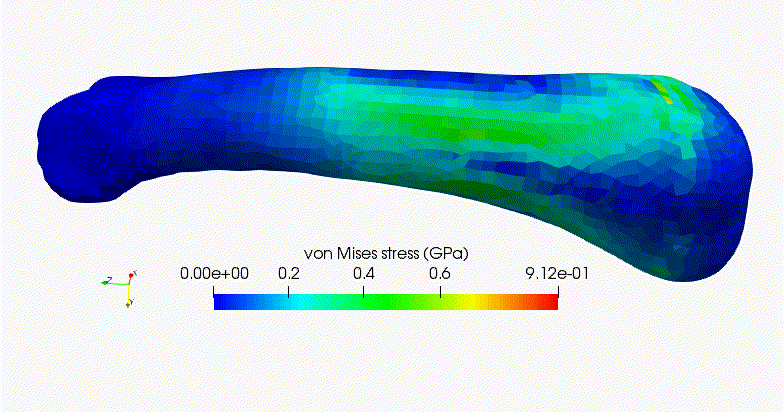
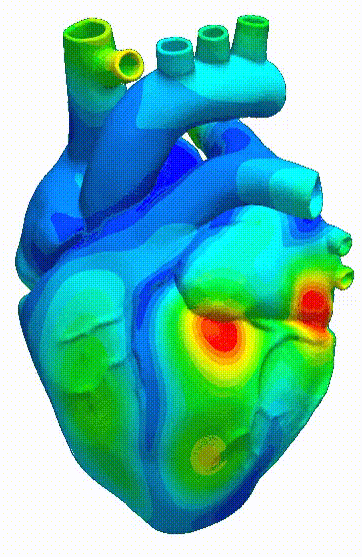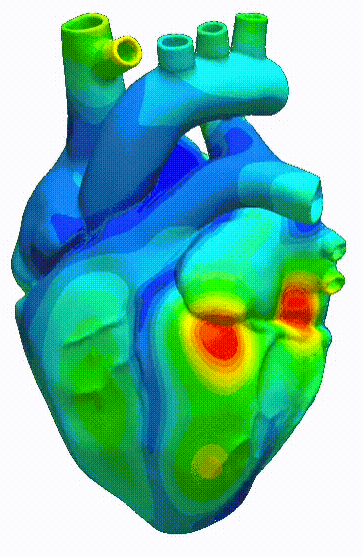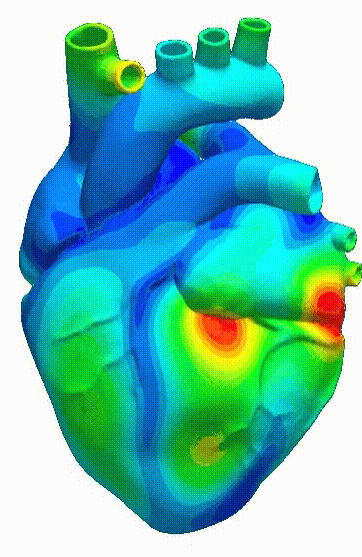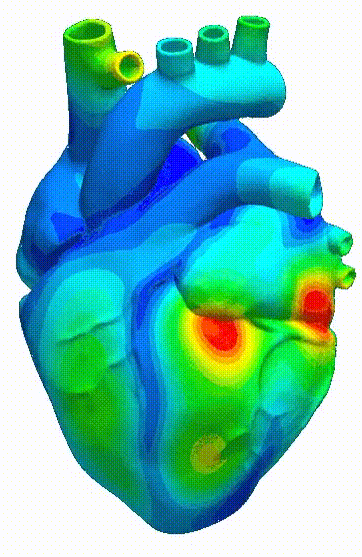Stereolithography (STL)- based analysis Stereolithography (STL) file format has been used widely in 3D printing. An automatic meshing algorithm for STL files is developed based on octree structure. Analysis of new designs drawn with CAD-based software can be performed with minimal effort.
Domain decomposition A novel coupling method for non-matching meshes is developed using arbitrary polyhedron elements. On the interface of the non-matching meshes, a surface mesh of polygon elements is constructed by merging the non-matching meshes. A shifting procedure is designed to prevent distortion. The solid elements connected to the interface are modified by replacing their faces on the interface with the new polygon elements, leading to matching discretization on the interface.
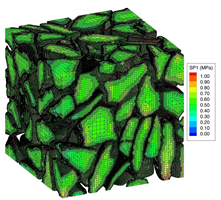
Fracture mechanics SBFEM excels in modelling fracture problems owing to its ability to represent singular solutions in the radial directions around the crack tip accurately. Fracture parameters such as stress intensity factors and T-stress can be extracted directly. Crack propagation modelling in various materials including piezoelectric plates can be performed with ease.
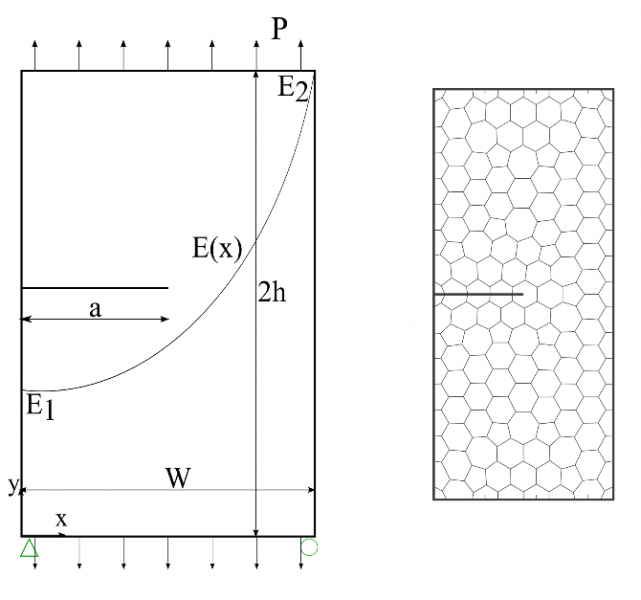
Functionally-graded materials Scaled boundary finite element shape functions for any star-convex polygonal shapes are developed. Singular stress fields can be represented accurately in the radial direction. Heterogenous material response in functionally-graded material can be represented analytically based on the radial coordinates.
Plate and shell 3D-consistent technique to analyse piezoelectric plates is developed based on scaled boundary finite element method. The in-plane problem geometry is meshed with 2D elements while the thickness direction is represented by matrix exponential function.
Contact mechanics A node-to-node (NTN) scheme for modelling contact problems within a scaled boundary finite element method (SBFEM) framework is developed. Nonmatching meshes can be simply converted into matching ones by appropriate node insertion, thereby allowing the use of the favourable NTN contact scheme. The general frictional contact is explicitly formulated as a mixed complementarity problem (MCP) with non-penetration and stick-slide exactly satisfied
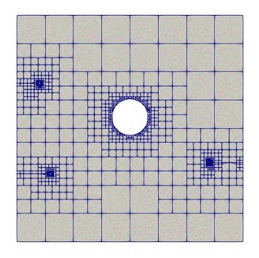
Damage mechanics Nonlocal damage model can be performed using scaled boundary finite element method both in 2D and 3D. The automatic octree mesh generation is employed to refine the mesh at the localised process zone (DPZ). One-point integration method is employed for efficient analysis.
Elastoplastic analysis The SBFEM is also capable of performing elastoplastic analysis. The automatic mesh generation techniques and one-point integration method allow the SBFEM to model the elastoplastic behaviours of complex structures efficiently.
Acoustic-structure interaction Various engineering applications are related to acoustic-structure interaction analysis, such as: dam-reservoir interaction, acoustic design of vehicles, air-coupled ultrasonic testing. The acoustic domain, such as the reservoir and air, can be infinitely large. It is advantageous to use SBFEM to model such an unbounded domain.
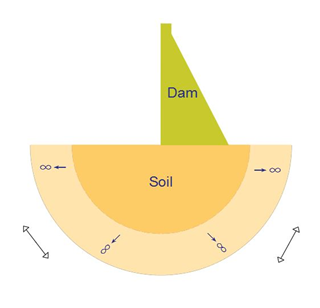
Soil-structure interaction The dynamic behaviour of the structure under a specific load is impacted by the physical property of the soil, and the presence of the structure in turn influences the response of the soil. SBFEM is suitable in modelling such problem as its polytope elements allows each part of the problem geometry, i.e. the soil and the structure, to be modelled separately and combined easily for analysis. The method is also efficient in modelling the far-field of the soil due to its analytical solution in radial direction.